来源:登链社区
为工作程序员提供的 ZKP 教程介绍。
你知道为什么斑马有条纹吗?一种理论是这是一种伪装。当斑马聚集在一起时,这使得狮子更难以区分它们的猎物。狮子必须将猎物从群体中隔离出来才能追捕它[^1]。
人类也喜欢在人群中隐藏。一个具体的例子是,当多个人在一个集体名称下作为一个整体行动时。《联邦党人文集》就是这样创作的[^2]。 另一个例子是 Bourbaki,这是 1930 年代一群法国数学家的集体笔名。这导致了现代数学大部分内容的彻底重写,重点在于严谨性和公理化方法[^3]。
在数字时代,假设你在一个群聊中,想要发送一条有争议的信息。你想证明你是其中的一员,而不透露是哪一位。我们如何在数字领域使用密码学来做到这一点?我们可以使用一种叫做 群签名 的东西。
从传统上讲,群签名在数学上相当复杂且难以实现。然而,使用零知识证明(ZKP),这个数学问题变成了一个简单的编程任务。在本文结束时,你将能够自己编写群签名。
介绍
这篇文章将向你展示如何从零开始编写基本的零知识证明(ZKP)。
在学习新的技术栈时,我们希望尽快掌握编辑-构建-运行的循环。只有这样,我们才能开始从自己的经验中学习。
我们将首先让你设置环境,编写一个简单的程序,执行所谓的可信设置,然后尽快生成和验证证明。之后,我们将识别一些改进我们程序的方法,实施这些改进并进行测试。在此过程中,我们将建立一个更好的心理模型,以便在实践中编程 ZKP。最后,你将熟悉(某种方式)从零开始编写 ZKP。
我们将逐步构建一个简单的签名方案,你可以证明你发送了特定的消息。你将能够理解这段代码的作用及其原因:
<span 1="" 9="" 18="" 10px="" 40px="" no-repeat="" height:="" width:="" margin-bottom:="" border-radius:="" code="" template="" signmessage="" signal="" input="" output="" component="" identityhasher="Poseidon(<span" span="" identity_commitment="==" signaturehasher="Poseidon( # 克隆仓库并运行准备脚本
git clone git@github.com:oskarth/zkintro-tutorial.git
cd zkintro-tutorial
# 在执行之前浏览此文件的内容
less ./scripts/prepare.sh
./scripts/prepare.sh
我们建议你浏览 ./scripts/prepare.sh 的内容,以查看这将安装什么,或者如果你更喜欢手动安装。执行后,你应该看到 Installation complete 并且没有错误。
如果你遇到问题,请查看最新的官方文档 这里[7]。完成后,你应该安装以下版本(或更高版本):
pragma circom 2.0.0;
template Multiplier2 () {
signal input a;
signal input b;
signal output c;
c <== a * b;
}
component main = Multiplier2();
这就是我们的特殊程序或 _电路_。 [^6] 按行分析:
-
pragma circom 2.0.0;– 定义所使用的 Circom 版本 -
template Multiplier()– 模板是大多数编程语言中对象的等价物,是一种常见的抽象形式 -
signal input a;– 我们的第一个输入,a;输入默认是私有的 -
signal input b;– 我们的第二个输入,b;同样默认是私有的 -
signal output b;– 我们的输出,c;输出始终是公共的 -
c <== a * b;– 这做了两件事:将信号c赋值 并 约束c等于a和b的乘积 -
component main = Multiplier2()– 实例化我们的主组件
最重要的行是 c <== a * b;。这是我们实际声明约束的地方。这个表达式实际上是两个的组合:<--(赋值)和 ===(等式约束)。 [^7] Circom 中的约束只能使用涉及常量、加法或乘法的操作。它强制要求方程的两边必须相等。 [^8]
关于约束
约束是如何工作的?在类似数独的上下文中,我们可能会说一个约束是“一个介于 1 和 9 之间的数字”。然而,在 Circom 的上下文中,这不是一个单一的约束,而是我们必须使用一组更简单的等式约束(===)来表达的东西。 [^9]
为什么会这样?这与底层的数学原理有关。从根本上讲,大多数 ZKP 使用 _算术电路_,它表示对 多项式 的计算。在处理多项式时,你可以轻松引入常量,将它们相加、相乘并检查它们是否相等。 [^10] 其他操作必须用这些基本操作来表达。你不必详细了解这一点才能编写 ZKP,但了解底层发生的事情可能会很有用。 [^11]
我们可以将电路可视化如下:
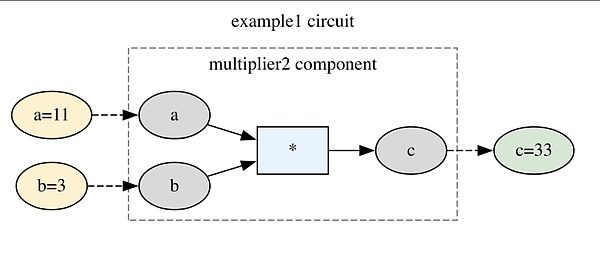
构建我们的电路
供你参考,最终文件可以在 example1-solution.circom 中找到。有关语法的更多详细信息,请参见 官方文档[9]。
我们可以通过运行以下命令来编译我们的电路:
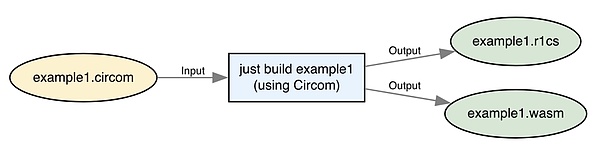
这是调用 circom 创建 example1.r1cs 和 example1.wasm 文件的一个简单包装。你应该会看到类似以下内容:
{
"pi_a": ["15932[...]3948", "66284[...]7222", "1"],
"pi_b": [
["17667[...]0525", "13094[...]1600"],
["12020[...]5738", "10182[...]7650"],
["1", "0"]
],
"pi_c": ["18501[...]3969", "13175[...]3552", "1"],
"protocol": "groth16",
"curve": "bn128"
}
这以一些数学对象(三个椭圆曲线元素)pi_a、pi_b 和 pi_c 的形式指定了证明。[^20] 它还包括有关协议(groth16)和使用的 _curve_(bn128,我们暂时忽略的数学实现细节)的元数据。这使得验证者知道如何处理此证明以正确验证。
请注意,证明是多么简短;无论我们的特殊程序多么复杂,它的大小都只有这个。这展示了我们在 _友好的零知识证明介绍_[10] 中讨论的 ZKP 的 succinctness 属性。上述命令还输出了我们的 _公共输出_:
这是与我们的见证和电路对应的所有公共输出的列表。在这种情况下,有一个公共输出对应于 c:33。[^21]
我们证明了什么?我们知道两个秘密值 a 和 b,它们的乘积是 33。这展示了我们在上一篇文章中讨论的 隐私 属性。
请注意,证明在孤立状态下没有用,它需要随之而来的公共输出。
验证证明
接下来,让我们验证这个证明。运行:
just verify_proof example1
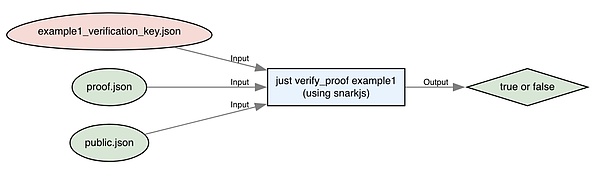
这需要验证密钥、公共输出和证明。通过这些,我们能够验证证明。它应该打印“证明已验证”。请注意,验证者从未接触到任何私有输入。
如果我们更改输出会发生什么?打开 example1/target/public.json,将 33 更改为 34,然后再次运行上述命令。
你会注意到证明不再被验证。这是因为我们的证明并没有证明我们有两个数字,其乘积是 34。
恭喜你,你现在已经编写了你的第一个 ZKP 程序,进行了可信设置,生成了证明并最终验证了它!
练习
-
ZKP 的两个关键属性是什么,它们意味着什么?
-
证明者的角色是什么,她需要什么输入?验证者呢?
-
解释
c <== a * b;这一行的作用。 -
为什么我们需要进行可信设置?我们如何使用其产物?
-
代码:完成
example1,直到你生成并验证了一个证明。
第二次迭代
通过上述电路,我们证明了我们知道两个(秘密)数字的乘积。这与 质因数分解 问题密切相关,这是许多密码学的基础。[^22] 这个想法是,如果你有一个非常大的数字,找到两个质数使其乘积等于这个大数字是很困难的。相反,检查两个数字的乘积是否等于另一个数字是非常简单的。[^23]
然而,我们的电路存在一个大问题。你能看到吗?
我们可以轻松地将输入更改为“1”和“33”。也就是说,一个数字 c 始终是 1 和 c 的乘积。这一点并不令人印象深刻,对吧?
我们想要做的是添加另一个 _约束_,使得 a 或 b 不能等于 1。这样,我们就被迫进行适当的整数因式分解。
我们如何添加这个约束,需要做哪些更改?
更新我们的电路
我们将为这些更改使用 example2 文件夹。不幸的是,我们不能仅仅写 a !== 1,因为这不是一个有效的约束。[^24] 它不是由常量、加法、乘法和等式检查组成的。我们如何表达“某物不是”?
这并不是立即直观的,这种类型的问题是编写电路的艺术所在。发展这种技能需要时间,并超出了本初始教程的范围;幸运的是,有许多好的资源可以参考。[^25]
不过,有一些常见的习语。基本的想法是使用 IsZero() 模板来检查一个表达式是否等于零。它对真值输出 1,对假值输出 0。
使用真值表[^26] 来显示可能的值通常是有帮助的。以下是 IsZero() 的真值表:
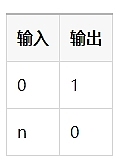
这是一个如此有用的构建块,以至于它被包含在 Circom 的库 circomlib 中。在 circomlib 中还有许多其他有用的组件。[^27]
我们可以通过创建一个 npm 项目(JavaScript)并将其作为依赖项添加来包含它。在 example2 文件夹中,我们已经为你完成了这一步。要导入相关模块,我们在 example2.circom 的顶部添加以下行:
include "circomlib/circuits/comparators.circom";
使用 IsZero(),我们可以检查 a 或 b 是否等于 1。修改 example2.circom 文件,使其包含以下行:
<span 1="" 12="" 4000="" 10px="" 40px="" no-repeat="" height:="" width:="" margin-bottom:="" border-radius:="" code="" component="" iszerocheck="IsZero();just generate_proof example2
just verify_proof example2
它仍然按预期生成和验证证明。
如果我们将 example2/input.json 的输入更改为 1 和 33 并尝试运行上述命令,我们将看到一个断言错误。也就是说,Circom 甚至不会让我们生成证明,因为输入违反了我们的约束。
完整流程图
现在我们已经经历了整个流程两次,让我们退后一步,看看所有部分是如何结合在一起的。
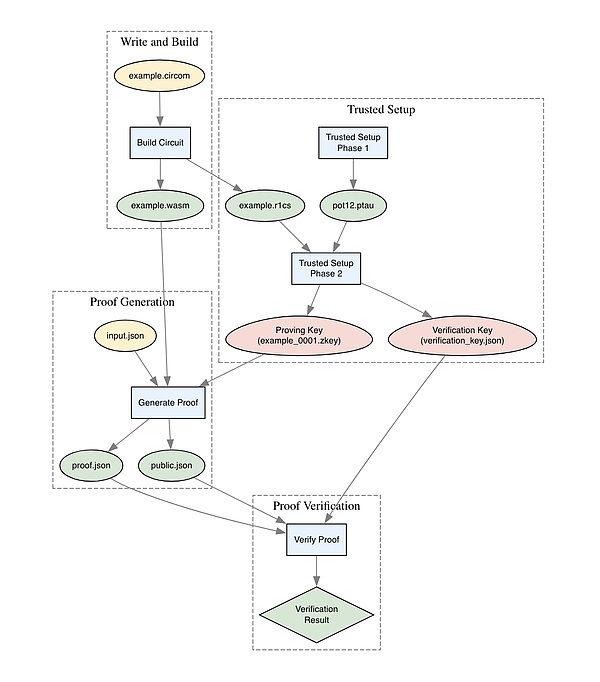
希望事情开始变得有些明朗。接下来,让我们提升一下,让我们的电路更有用。
练习
-
为什么我们必须运行
example2的第 2 阶段,而不是第 1 阶段? -
上一个例子的主要问题是什么,我们是如何解决的?
-
代码:完成
example2,直到你无法生成证明。
第三次迭代
通过上述电路,我们已经证明了我们知道两个秘密值的乘积。单靠这一点并不是很有用。在现实世界中,有用的是 _数字签名方案_。通过它,你可以向其他人证明你写了特定的消息。我们如何使用 ZKP 来实现这一点?要实现这一点,我们必须首先涵盖一些基本概念。
现在是短暂休息的好时机,去喝一杯你最喜欢的饮料。
数字签名
数字签名已经存在,并且在我们的数字时代无处不在。现代互联网没有它们是无法运作的。通常,这些是使用 公钥密码学 实现的。在公钥密码学中,你有一个私钥和一个公钥。私钥仅供你自己使用,而公钥是公开共享的,代表你的身份。
数字签名方案由以下部分组成:
-
密钥生成:生成一个私钥和相应的公钥
-
签名:使用私钥和消息创建签名
-
签名验证:验证消息是否由相应的公钥签名
虽然具体细节看起来不同,但我们编写的程序和上述密钥生成算法共享一个共同元素:它们都使用 _单向函数_,更具体地说是 _陷门函数_。陷门是容易掉进去但难以爬出来的东西(除非你能找到一把隐藏的梯子) [^30]。
对于公钥密码学,从私钥构造公钥是容易的,但反过来却非常困难。我们的前一个程序也是如此。如果这两个秘密数字是非常大的质数,那么将该乘积转回原始值是非常困难的。现代公钥密码学通常在底层使用 _椭圆曲线密码学_。
传统上,创建像这些数字签名方案这样的密码协议需要大量的工作,并需要提出一个涉及一些巧妙数学的特定协议。我们不想这样做。相反,我们想使用 ZKP 编写一个程序,以实现相同的结果。
而不是这样:[^31]

我们只想编写一个程序,生成我们想要的证明,然后验证这个证明。
哈希函数和承诺
我们将使用两个更简单的工具:_哈希函数_ 和 _承诺_,而不是使用椭圆曲线密码学。
哈希函数也是一种单向函数。例如,在命令行中,我们可以这样使用 SHA-256 哈希函数:
commitment = hash(some_secret)
signature = hash(some_secret, message)
此时你可能有一些问题。让我们解决一些你脑海中可能存在的问题。
首先,为什么这有效,我们为什么需要 ZKP?当有人验证证明时,他们只能访问承诺、消息和签名。没有直接的方法可以验证承诺是否对应于秘密,而不揭示秘密。在这种情况下,我们只是在生成证明时“揭示”秘密,因此我们的秘密保持安全。
其次,为什么在 ZKP 内部使用这些哈希函数和承诺,而不是公钥密码学?你绝对可以在 ZKP 内部使用公钥密码学,并且这样做是有合理理由的。就约束而言,它的实现成本远高于上述方案。这使得它比上述更慢,更复杂。正如我们将在下一节中看到的,哈希函数的选择非常重要。
最后,为什么在我们已经拥有公钥密码学的情况下还要使用 ZKP?在这个简单的例子中,没有必要使用 ZKP。然而,它作为更有趣的应用的构建块,例如本文开头提到的群签名示例。毕竟,我们想要 _编程密码学_。
这真是太多了!幸运的是,我们已经过了难关。让我们开始编码吧。如果你一开始没有完全理解上述内容,也不用担心。习惯这种推理方式需要一些时间。
回到代码
我们将从 example3 目录开始工作。
要实现数字签名,我们需要做的第一件事是生成我们的密钥。这些对应于公钥密码学中的私钥和公钥。由于密钥对应于一个身份(你,证明者),我们将分别称其为 identity_secret 和 identity_commitment。它们共同形成一个身份对。
这些将作为电路的输入,与我们要签名的消息一起使用。作为公共输出,我们将拥有签名、承诺和消息。这将允许某人验证签名确实是正确的。
由于我们需要身份对作为电路的输入,因此我们将单独生成这些:just generate_identity
这会产生类似于以下内容:
include "circomlib/circuits/poseidon.circom";
Poseidon 哈希模板的使用如下:
<span 10px="" 40px="" no-repeat="" height:="" width:="" margin-bottom:="" border-radius:="" code="" component="" hasher="Poseidon(2);component main {public [identity_commitment, message]} = SignMessage();
默认情况下,我们电路的所有输入都是私有的。通过这个,我们明确标记 identity_commitment 和 message 为公共。这意味着它们将成为公共输出的一部分。
有了这些信息,你应该有足够的知识来完成 example3.circom 电路。如果你仍然卡住,可以参考 example3-solution.circom 获取完整代码。
像之前一样,我们必须构建电路并运行受信任设置的第 2 阶段:
{
"identity_secret": "21879[...]1709",
"identity_commitment": "48269[...]7915",
"message": "42"
}
随意将身份对更改为你自己使用 just generate_identity 生成的身份对。毕竟,你想把身份秘密保留给自己!
你可能会注意到消息只是一个作为字符串引用的数字 ("42")。不幸的是,由于约束在数学上的工作方式(使用线性代数和 _算术电路_),我们只能使用数字而不能使用字符串。电路内部支持的唯一操作是基本的算术操作,如加法和乘法。[^37]
我们现在可以生成和验证一个证明:
["48968[...]5499", "48269[...]7915", "42"]
这分别对应于签名、承诺和消息。
让我们看看如果我们不小心,事情可能会出错。 [^38]
首先,如果我们将身份承诺更改为 input.json 中的随机内容,会发生什么?你会注意到我们无法再生成证明。这是因为我们还在电路内部检查身份承诺。保持身份秘密和承诺之间的关系至关重要。
其次,如果我们不将消息包含在输出中,会发生什么?我们确实得到了一个证明,并且它得到了验证。但消息可以是 _任何东西_,因此它实际上并不能证明你发送了特定的消息。类似地,如果我们不将身份承诺包含在公共输出中,会发生什么?这意味着身份承诺可以是任何东西,因此我们实际上不知道 谁 签署了消息。
作为思考练习,想想如果我们省略这两个关键约束中的任何一个会发生什么:
-
identity_commitment === identityHasher.out -
signature <== signatureHasher.out
恭喜你,现在你知道如何编程加密了![^39]
练习
-
数字签名方案的三个组成部分是什么?
-
使用像 Poseidon 这样的 “ZK-Friendly hash function” 的目的是什么?
-
什么是承诺?我们如何将它们用于数字签名方案?
-
为什么我们将身份承诺和消息标记为公共?
-
为什么我们需要身份承诺和签名约束?
-
代码:完成
example3,直到你生成并验证了一个证明。
下一步
通过上述数字签名方案,以及我们在文章中看到的一些技巧,你拥有了实现文章开头提到的 群签名方案 的所有工具。[^40]
在 example4 中存在骨架代码。你只需要 5-10 行代码。唯一的新语法是 for 循环,它的工作方式与大多数其他语言相同。[^41]。
这个电路将允许你:
-
签署一条消息
-
证明你是三个人之一(身份承诺)
-
但不透露是哪一个
你可以把它看作一个谜题。关键的见解基本上归结为一个算术表达式。如果可以的话,尝试在纸上解决它。如果你卡住了,可以像之前一样查看解决方案。
最后,如果你想要一些额外的挑战,这里有一些扩展的方法:
-
允许组内任意多的人
-
实现一个新的电路
reveal,证明你签署了特定的消息 -
实现一个新的电路
deny,证明你没有签署特定的消息
使用经典工具创建这样的加密协议将是一项巨大的任务,需要大量的专业知识。[^42] 使用 ZKP,你可以在一个下午变得高效和危险,将这些问题视为编程任务。这只是我们可以做的冰山一角。
练习
-
群签名与普通签名有什么不同?它们可以如何使用?
问题
这些问题是可选的,需要更多的努力。
-
找出
IsZero()是如何实现的。 -
代码:完成上述群签名方案(见
example4)。 -
代码:扩展上述群签名示例:允许更多人并实现
reveal和/或deny电路。 -
你将如何设计一个 “ZK 身份” 系统来证明你已满 18 岁?你可能想证明的其他属性是什么?从高层次来看,你将如何实现它,以及你看到的挑战是什么?研究现有解决方案以更好地理解它们是如何实现的。
-
对于像以太坊这样的公共区块链,有时会使用 Layer 2 (L2) 来允许更快、更便宜和更多的交易。从高层次来看,你将如何使用 ZKP 设计一个 L2?解释你看到的一些挑战。研究现有解决方案以更好地理解它们是如何实现的。## 结论
在本教程介绍中,我们熟悉了如何从头开始编写和修改基本的零知识证明(ZKPs)。我们设置了编程环境并编写了一个基本电路。然后我们进行了可信设置,创建并验证了证明。我们识别了一些问题并改进了电路,确保测试我们的更改。之后,我们使用哈希函数和承诺实现了一个基本的数字签名方案。
我们还学习了足够的技能和工具,以便能够实现群体签名,这在没有零知识证明的情况下是很难实现的。
我希望你对编写零知识证明所涉及的内容有了更好的心理模型,并对实际中的编辑-运行-调试周期有了更好的理解。这将为你将来可能编写的任何其他零知识证明程序打下良好的基础,无论你最终使用什么技术栈。
致谢
感谢 Hanno Cornelius、Marc Köhlbrugge、Michelle Lai、lenilsonjr 和 Chih-Cheng Liang 阅读草稿并提供反馈。
图片
-
Bourbaki Congress 1938 – 未知,公有领域,通过 Wikimedia[11]
-
Hartmann’s Zebras – J. Huber,CC BY-SA 2.0,通过 Wikimedia[12]
-
Trapdoor Spider – P.S. Foresman,公有领域,通过 [Wikimedia](https://commons.wikimedia.org/wiki/File:Trapdoor_(PSF “Wikimedia”).png)
-
Kingsley Lockbox – P.S. Foresman,公有领域,通过 Wikimedia[13]
参考资料
[1] AI翻译官: https://learnblockchain.cn/people/19584
[2] 翻译小组: https://learnblockchain.cn/people/412
[3] learnblockchain.cn/article…: https://learnblockchain.cn/article/9178
[4] 零知识的友好介绍: https://learnblockchain.cn/article/6184
[5] git 仓库: https://github.com/oskarth/zkintro-tutorial
[6]git 仓库: https://github.com/oskarth/zkintro-tutorial
[7]这里: https://docs.circom.io/getting-started/installation/
[8]zkrepl.dev: https://zkrepl.dev/
[9]官方文档: https://docs.circom.io/circom-language/signals/
[10]友好的零知识证明介绍: https://learnblockchain.cn/article/6184
[11]Wikimedia: https://commons.wikimedia.org/wiki/File:Bourbaki_congress1938.png
[12]Wikimedia: https://commons.wikimedia.org/wiki/File:Hartmann_zebras_hobatereS.jpg
[13]Wikimedia: https://commons.wikimedia.org/wiki/File:Kingsley_lockbox.jpg
[14]AI 翻译官: https://learnblockchain.cn/people/19584
[15]这里: https://github.com/lbc-team/Pioneer/blob/master/translations/9178.md
[16]^2]: 参见 [联邦党人文集(维基百科): https://en.wikipedia.org/wiki/The_Federalist_Papers#Authorship
[17]^3]: 参见 [Bourbaki(维基百科): https://en.wikipedia.org/wiki/Nicolas_Bourbaki#Membership
[18]^8]: 这使得编写约束相当具有挑战性,正如你可以想象的那样。有关 Circom 中约束的更多详细信息,请参见 [https://docs.circom.io/circom-language/constraint-generation/: https://docs.circom.io/circom-language/constraint-generation/
[19]^12]: 线性约束意味着它可以仅通过加法表示为线性组合。这相当于使用常数进行乘法。需要注意的主要是线性约束比非线性约束更简单。有关更多详细信息,请参见 [约束生成: https://docs.circom.io/circom-language/constraint-generation/
[20]算术电路: https://docs.circom.io/background/background/#arithmetic-circuits
[21]^13]: 从数学上讲,我们所做的是确保方程 Az * Bz = Cz 成立,其中 Z=(W,x,1)。A、B 和 C 是矩阵,W 是见证(私有输入),x 是公共输入/输出。虽然知道这一点很有用,但编写电路时并不需要理解这一点。有关更多详细信息,请参见 [Rank-1 约束系统: https://docs.circom.io/background/background/#rank-1-constraint-system
[22]^15]: 正如在 友好的介绍 文章中提到的那样,2016 年 Zcash 举办的仪式有一个很好的外行播客,你可以在 [这里: https://radiolab.org/podcast/ceremony
[23]^17]: 我们称之为 1-out-of N 信任模型。还有许多其他信任模型;你最熟悉的可能是多数规则,即你信任大多数人做出正确的决定。这基本上就是民主和大多数投票的运作方式。 [↩: #user-content-fnref-17
[24]^22]: 也称为 _密码学难度假设_。请参见 [计算难度假设 (维基百科): https://en.wikipedia.org/wiki/Computational_hardness_assumption#Common_cryptographic_hardness_assumptions
[25]^23]: 有关更多信息,请参见 [https://en.wikipedia.org/wiki/Integer_factorization: https://en.wikipedia.org/wiki/Integer_factorization
[26]^24]: 虽然我们可以添加 _asserts_,但这些实际上不是约束,仅用于清理输入。有关其工作原理,请参见 [https://docs.circom.io/circom-language/code-quality/code-assertion/: https://docs.circom.io/circom-language/code-quality/code-assertion/
[27]https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions: https://www.chainsecurity.com/blog/circom-assertions-misconceptions-and-deceptions
[28]^25]: 这份由 0xPARC 提供的资源非常出色,如果你想深入了解编写 (Circom) 电路的艺术: [https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/: https://learn.0xparc.org/materials/circom/learning-group-1/circom-1/
[29]^26]: 由于编写约束的性质,这种情况经常出现。请参见 [https://en.wikipedia.org/wiki/Truth_table: https://en.wikipedia.org/wiki/Truth_table
[30]^27]: 有关 circomlib 的更多信息,请参见 [https://github.com/iden3/circomlib: https://github.com/iden3/circomlib
[31]^28]: 请参见 [https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom: https://github.com/iden3/circomlib/blob/master/circuits/comparators.circom
[32]^29]: 人们通常在项目之间共享这些 ptau 文件以提高安全性。有关详细信息,请参见 [https://github.com/privacy-scaling-explorations/perpetualpowersoftau: https://github.com/privacy-scaling-explorations/perpetualpowersoftau
[33]https://github.com/iden3/snarkjs: https://github.com/iden3/snarkjs
[34]^30]: 这里的梯子代表某种值,使我们能够以相反的“困难”方式进行。另一种思考方式是将其视为一个挂锁。你可以轻松锁定它,但很难解锁,除非你有钥匙。陷门函数也有更正式的定义,请参见 [https://en.wikipedia.org/wiki/Trapdoor_function: https://en.wikipedia.org/wiki/Trapdoor_function
[35]^31]: 来自维基百科的截图。请参见 [ECDSA (维基百科): https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm#Signature_verification_algorithm
[36]^38]: 在现实世界的数字签名方案中,当多个消息交换时,我们可能还希望引入一个加密随机数。这是为了避免重放攻击,即某人可以在稍后时间重用相同的签名。请参见 [https://en.wikipedia.org/wiki/Replay_attack: https://en.wikipedia.org/wiki/Replay_attack
[37]^40]: 在 ZKP 中实现群签名的灵感来自 0xPARC,请参见 [https://0xparc.org/blog/zk-group-sigs: https://0xparc.org/blog/zk-group-sigs
[38]^41]: 请参见 [https://docs.circom.io/circom-language/control-flow/: https://docs.circom.io/circom-language/control-flow/
[39]^42]: 相比之下,实施群签名的论文如 [https://eprint.iacr.org/2015/043.pdf: https://eprint.iacr.org/2015/043.pdf

+ There are no comments
Add yours